
Todd W. Neller, Gettysburg College Department of Computer Science

| Summary | FairKalah: fair Mancala competition - Students experientially learn about alpha-beta pruning, heuristic evaluation, and time management in real-time, fair Mancala competition. |
| Topics | game-tree search, minimax, alpha-beta pruning, heuristic evaluation, time management, bounded rationality |
| Audience | Introductory Artificial Intellegence (AI) students |
| Difficulty | Suitable for an upper-level undergraduate or graduate course with a focus on AI programming |
| Strengths | In providing 254 fair initial board positions, we enable better evaluation of real-time, game-playing AI. In Mancala and some other games commonly used in AI education, a first-player advantage obscures evaluation of relative AI player strength. In this unusual first release of research results via an assignment, we fix an unfair, common, accessible game to give it fresh life for use in the classroom. |
| Weaknesses | Code is currently only available in Java, Python, and Ludii. (Ports to other languages are invited!) |
| Dependencies | Students must have intermediate undergraduate programming skill and become familiar with the concepts of the relevant readings below. |
| Variants | There are many variants of Mancala (a.k.a. Kalah), and game play may be modified with the caveat that given fair board positions would no longer be expected to be fair under a different rule set. Having 254 fair initial game states allows for variety of game play. |
Video presentation of the rules (5:52) and a complete demonstration game (6:20)
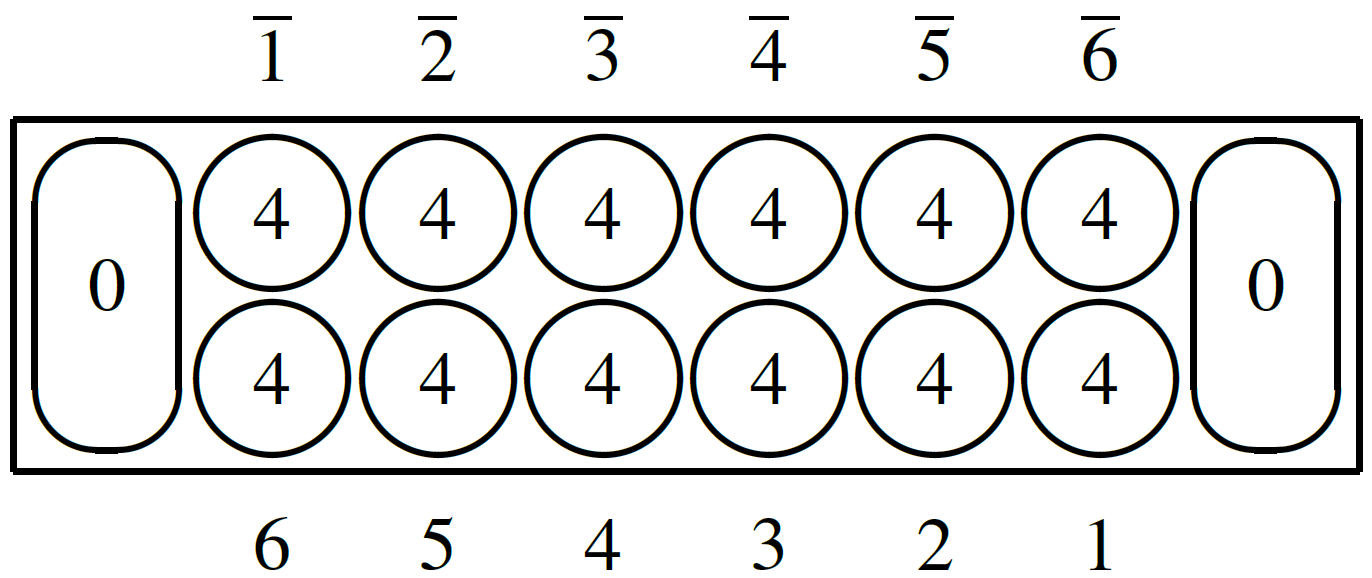
Materials: Mancala (a.k.a. Kalah) is played on a rectangular board as depicted above with 6 play pits for each player along the long side and 1 score pit ("Kalah") for each player on the player's right-hand end of the board. In the standard initial board state, each of the play pits starts with 4 pieces (a.k.a. seeds) per pit. We refer to play pits by the number of pits they are clockwise away from the player's score pit. (Pits of the second player (north) are notated with overbars. Numbers depicted within pits indicate the number of pieces in that pit.)Play: On a player's turn, the player selects one of their play pits containing pieces, removes all pieces from that play pit, and redistributes ("sows") them counterclockwise, one piece per play/score pit, and skipping their opponent's score pit. If the last piece redistributed lands in the score pit, the player takes another turn; otherwise, it becomes the opponent's turn. If the last piece redistributed lands in an empty play pit of the player (including after having redistributed pieces to all opponent play pits), then that piece captures: both that piece and any pieces in the opponent's opposite play pit are removed from the pits and placed into the player's score pit.
Game End: The game ends when, at the end of a turn, there are no pieces left in one player's play pits. Their opponent scores any remaining pieces in play pits. The player with more pieces in their score pit wins. If the number of pieces in the score pits are the same, the players draw (i.e. tie) the game.
One can observe example game play with this plain text game transcript. Note how we interpret the original patent rules with regards to the final "empty capture" or "zero capture". The original rule text of both the patent and the 1958 Kalah Game Company rules have only the "if" condition that the last piece lands in a player's empty play pit. There appears to be no requirement that there be opponent pieces to capture. This is consistent with the research interpretation of Irving, Donkers, and Uiterwijk. Without this empty/zero-capture rule, the last move taken would not result in a capture.
It is also worth noting that the last move leaves the first player's side empty, yet the opponent has a legal move. In some variants, the game ends when the a player has no legal moves on their turn, which is known as "starvation". As one can see in this transcript, if we didn't end the game when either player's play pits are empty, then the second (north) player's turn would necessarily redistribute pieces to the first (south) player's play pits. Both the original patent rules and the 1958 Kalah Game Company rules clearly end the game "when all of the pits on one side of the game board are empty" and "when all six pits on one side are empty", respectively.
Included in the assignment materials is the ability to initialize Mancala boards to one of 254 fair initial states. FairKalah is the name we use for Mancala/Kalah played from a fair initial state. For the standard initial state of 4 pieces per pit, perfect play that optimizes final score will result in the first player winning 29 to 19, a difference of 10 points. Thus, standard Mancala is unfair, giving advantage to the first player.
In each of the provided 254 FairKalah initial states, perfect play that optimizes final score will result in a draw (24 to 24). These 254 initial states show all of the possible ways that one can move one or two pieces from the standard initial state to other play or score pits so as to achieve fairness.
These fair initial states were found by computing the game value of each possible redistribution of one or two pieces and retaining only those with a game value of 0 (draw). Initial state evaluations were performed with our Java port of Geoffrey Irving's Mancala analysis code used for the paper Solving Mancala featuring zero-window alpha-beta search and a 24-piece endgame database we computed. This work was done in collaboration with Taylor Neller.
In this assignment, you will be provided with an implementation of a depth-limited minimax Mancala player that heuristically evaluates state values as the MAX (first/south) player score minus the MIN (second/north) player score. That is, both players are seeking to maximize their respective score lead against their opponent.
Your goal will be to implement the strongest Mancala AI within fixed real-time computation limits (e.g. 2.5 minutes maximum total reasoning time per game) and memory limits (e.g. 1MB memory for code and data, 1GB RAM at runtime) as specified by your instructor. This will be accomplished through three implementation tasks:
Instructor note: I generally assign this project to pairs of students for approximately two weeks, but one can also assign this individuals or larger groups, adjusting time accordingly. I encourage students to work together, making sure all understand the workings, performance data observations, and resulting design decisions for each part. Put simply, each student should be able to present each part of the resulting work.
There are many opportunities for simple research and innovation in this assignment.
For heuristic evaluation, you are encouraged to first play the game, either physically or via the Ludii General Game System. Start the game program (e.g. with command "java -jar Ludii-1.3.1.jar" or whichever more recent version exists), then File → Load Game (or Ctrl-L) → Games → board → sow → two rows → FairKalah.
Next, consider different possible features of game state beyond score different that could affect your evaluation, e.g. the relative number of player free moves, the relative player mobility (i.e. relative number of free moves), etc. The art of heuristic evaluation concerns the trade-off of time (for more complicated evaluation) for improved evaluation leading to better moves. Each feature considered must pull its computational weight in this trade-off, increasing game play performance. For this reason, implement early so as to leave plenty of time for experimentation and refinement. The most successful student AI Mancala player heuristic I have seen was a data-driven approach that selected and weighted simple, computationally inexpensive features according to collected play data.
Instructor notes:
fairkalah-maia-data.zip contains two files, fairkalah-maia-data.csv, a comma-separated value data file of board states with associated negamax game values and indications of optimal play(s), and fairkalah-maia-data-README.txt, a text file documenting the columns of the CSV data file.
There are a number of possible uses of this data for engineering a better FairKalah player. Here is a sketch of one: