Project 3: Fake News! 
For this project, you will build and analyze several algorithms for determining whether a headline is real or fake news.
Data: Fake and real news headlines
We have compiled 1298 “fake news” headlines (which mostly include headlines of articles classified as biased etc.) and 1968 “real” news headlines, where the “fake news” headlines are from https://www.kaggle.com/mrisdal/fake-news/data and “real news” headlines are from https://www.kaggle.com/therohk/million-headlines. We further cleaned the data by removing words from fake news titles that are not a part of the headline, removing special characters from the headlines, and restricting real news headlines to those after October 2016 containing the word “trump”. For your interest, the cleaning script is available at clean_script.py, but you do not need to run it. The cleaned-up data is available below:
- Real news headlines: clean_real.txt
- Fake news headlines: clean_fake.txt
Each headline appears as a single line in the data file. Words in the headline are separated by spaces, so just use str.split() in Python to split the headlines into words.
Part 1 (2 pts)
Describe the datasets. You will be predicting whether a headline is real or fake news from words that appear in the headline. Is that feasible? Give 3 examples of specific keywords that may be useful, together with statistics on how often they appear in real and fake headlines.
For the rest of the project, you should split your dataset into ~70% training, ~15% validation, and ~15% test.
Part 2 (20 pts)
Implement the Naive Bayes algorithm for predicting whether a headline is real or fake. Tune the parameters of the prior (called \(m\) and \(\hat{p}\) on slide 23 of the Generative Classifiers lecture) using the validation set. Report how you did it, and the result. Report the performance on the training and the test sets that you obtain. Note that computing products of many small numbers leads to underflow. Use the fact that \[a_ 1 a_ 2 ... a_ n = \exp(\log a_1 + \log a_2 + ... \log a_n)\] In your report, explain how you used that fact.
Part 3 (15 pts)
Part 3(a) (10 pts)
List the 10 words whose presence most strongly predicts that the news is real.
List the 10 words whose absence most strongly predicts that the news is real.
List the 10 words whose presence most strongly predicts that the news is fake.
List the 10 words whose absence most strongly predicts that the news is fake.
State how you obtained those in terms of the the conditional probabilities used in the Naive Bayes algorithm. Compare the influence of presence vs absence of words on predicting whether the headline is real or fake news.
Part 3(b) (3 pts)
You may find common words like “a”, “to”, and others in your list in Part 3(a). These are called stopwords. A list of stopwords is available in sklearn here. You can import this as follows:
from sklearn.feature_extraction.text import ENGLISH_STOP_WORDS
Now, list the 10 non-stopwords that most strongly predict that the news is real, and the 10 non-stopwords that most strongly predict that the news is fake.
Part 3(c) (2 pts)
Why might it make sense to remove stop words when interpreting the model? Why might it make sense to keep stop words?
Part 4 (15 pts)
Train a Logistic Regression model on the same dataset. For a single headline \(h\) the input to the Logistic Regression model will be a \(k\)-dimensional vector \(v\), where \(v[k]=1\) if the \(k\)-th keyword appears in the headline \(h\), and \(v[k]=0\) otherwise. The set of keywords consists of all the words that appear in all the headlines. You may use your implementation of Logistic Regression from the previous projects, or any other implementation of your choice.
Plot the learning curves (performance vs. iteration) of the Logistic Regression model. Describe how you selected the regularization parameter (and describe the experiments you used to select it).
Part 5 (5 pts)
At test time, both Logistic Regression and Naive Bayes can be formulated as computing
\[\theta_0 + \theta_1 I_1 (x) + \theta_2 I_2 (x) + ... + \theta_k I_k (x) > \text{thr}\]
in order to decide whether to classify the input \(x\) as \(1\) or \(0\). Explain, in each case, what the \(\theta\)’s and the \(I\)’s are.
Part 6 (13 pts)
Part 6(a) (5 pts)
In your report, display a list of top 10 positive \(\theta\)s and negative \(\theta\)s obtained from Logistic Regression, and the words that they correspond with. How do these lists compare with those in part 3(a)? Do you notice any similarities or differences?
Part 6(b) (3 pts)
Do the same as the previous part, but ignore all stop words. How do these lists compare with those in part 3(b)?
Part 6(c) (5 pts)
In this project, we used the magnitude of the logistic regression parameters to indicate importance of a feature. Why might this be a bad idea in general? (Hint: what if the features are not normalized?) Why is it reasonable to use the magnitude in this problem?
Part 7 (20 pts)
In this part, you will build a decision tree to classify real vs fake news headlines. Instead of coding the decision trees yourself, you will do what we normally do in practice – use an existing implementation. You should use the DecisionTreeClassifier included in sklearn. Note that figuring out how to use this implementation is a part of the assignment.
Here’s a link to the documentation of sklearn.tree.DecisionTreeClassifier
http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
Part 7(a) (10 pts)
Train the decision tree classifier. Show the relationship between the max_depth of the tree, and the training / test validation accuracy. You should try around 10 different values of max_depth. Choose the best-performing decision tree classifier for the following parts. Explain how you made the choice. Also, explain other parameters of DecisionTreeClassifier for which you are using non-default values, and how you determined those parameters.
Part 7(b) (5 pts)
Extract and visualize the first two layers of the tree. Your visualization may look something like what is shown below, but it does not have to be an image: it is perfectly fine to display text. Include your visualization in your report.
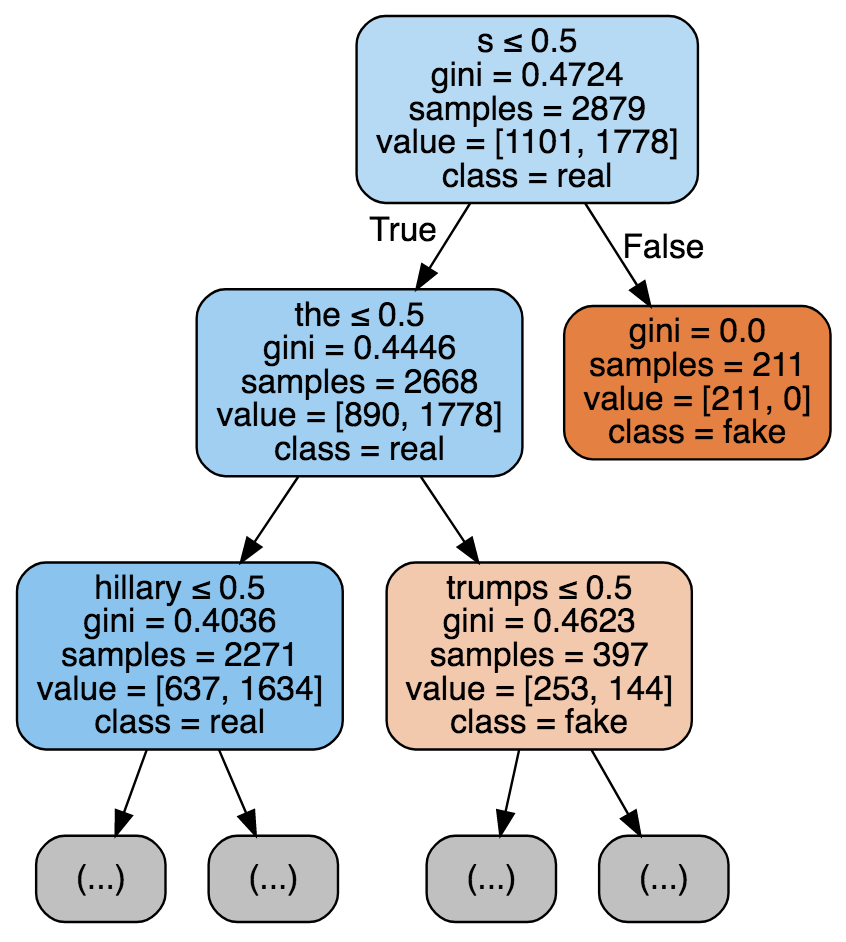
How do the most important features in Naive Bayes (Part 3a) and Logistic Regression (Part 6a) compare with the features chosen by the decision tree in your visualization.
Part 7(c) (5 pts)
Summarize the performance of your three classifiers on the training, validation, and test sets. Which classifier performed best? The worst? Which one overfit the most?
Part 8 (10 pts)
Part 8(a) (5 pts)
For the first split of your Decision Tree from Part 7, compute the mutual information of the split on the training data. That is, compute \(I(Y,x_i)\) where \(Y\) is the random variable signifying whether a headline is real or fake, and \(x_i\) is the keyword chosen for the top most split.
You can do this either by hand or by writing a function. In either case, include the code or all the steps involved in your computation in your writeup.
Part 8(b) (5 pts)
Choose another variable \(x_j \ne x_i\), and compute \(I(Y,x_j)\). Again, include all code or steps used in your computation in your writeup. How does this value compare to what you obtained in 8(a)?
What to submit
The project should be implemented using Python 2 or 3 and should be runnable on the CS Teaching Labs computers. Your report should be in PDF format. You should use LaTeX to generate the report, and submit the .tex file as well. A sample template is on the course website. You will submit at least the following files: fake.py, fake.tex, and fake.pdf. You may submit more files as well. You may submit ipynb files in place of py files.
Reproducibility counts! We should be able to obtain all the graphs and figures in your report by running your code. The only exception is that you may pre-download the images (what and how you did that, including the code you used to download the images, should be included in your submission.) Submissions that are not reproducible will not receive full marks. If your graphs/reported numbers cannot be reproduced by running the code, you may be docked up to 20%. (Of course, if the code is simply incomplete, you may lose even more.) Suggestion: if you are using randomness anywhere, use numpy.random.seed().
You must use LaTeX to generate the report. LaTeX is the tool used to generate virtually all technical reports and research papers in machine learning, and students report that after they get used to writing reports in LaTeX, they start using LaTeX for all their course reports. In addition, using LaTeX facilitates the production of reproducible results.
Available code
You are free to use any of the code available from the course website.
Readability
Readability counts! If your code isn’t readable or your report doesn’t make sense, they are not that useful. In addition, the TA can’t read them. You will lose marks for those things.
Academic integrity
It is perfectly fine to discuss general ideas with other people, if you acknowledge ideas in your report that are not your own. However, you must not look at other people’s code, or show your code to other people, and you must not look at other people’s reports and derivations, or show your report and derivations to other people. All of those things are academic offences.