Sudoku is a popular logic puzzle that consists of a square grid of width w, that can be divided symmetrically into subgrids, and a domain of distinct values of size equal to the puzzle width. The most common configuration is a 9 x 9 grid that can be divided into nine 3 x 3 subgrids, and a domain of 9 distinct values (usually the integers 1-9). This configuration is usually called a 3 x 3 puzzle, even though its dimensions are 9 squares by 9 squares. Another popular configuration is a 4 x 4 puzzle with dimensions of 16 squares by 16 squares, and that uses the 16 symbols of the hexadecimal number system (0-9 + A-F). The goal is to place the values from the domain such that the following constraints are obeyed:

1. Each row must contain one and only one occurrence of each distinct value.
2. Each column must contain one and only one ocurrence of each disinct value.
3. Each subgrid must contain one and only one occurrence of each distinct value.

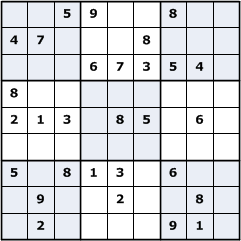
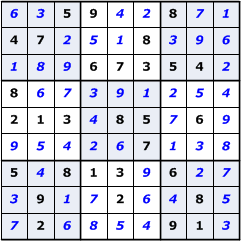
In the puzzle's initial state some of the values are typically already present, while the remaining squares are blank. Figure 1 shows an example of a 3 x 3 Sudoku puzzle in both its initial and solved states.

Figure 1. Example of a Sudoku puzzle. The diagram on the left represents the puzzle in its initial, unsolved state. Pre-assigned values are shown. The diagram on the right is the puzzle after it has been solved. The nine subgrids in the puzzle are shown using alternating blue and white backgrounds for the individual squares that make up the subgrids.

Suppose we want to construct an intelligent agent to solve any given 3 x 3 Sudoku puzzle. Given an empty starting grid there are 6,670,903,752,021,072,936,960 (or 6.67 x 10²¹) possible arrangements for the 9 values in the domain [1]. This value has been reduced to 5,472,730,538 distinct puzzles by filtering out symmetrical arrangements due to reflection and rotation [2]. Many of these arrangements will not produce solutions, as they will violate one or more of the puzzle's constraints.

An uninformed, brute force search would proceed by traversing the grid and systematically assigning values to the squares until a constraint has been violated, at which point the search would backtrack to the previous level and attempt the next value. If all of the legal values violate one or more constraints, the search must backtrack two levels, then three levels, etc., until a solution has been found. If the search is truly uninformed, all legal values would be considered as candidates for each square; i.e., no filtering out of illegal values would occur. Furthermore, an uninformed search would know nothing about the existence of symmetries caused by rotating or flipping the grid, so it would potentially need to work through all 6.67 x 10²¹ possible arrangements. It is obvious that an uninformed search is not practical for solving this problem; therefore, an informed agent is needed.

Since the order in which the squares are filled is irrelevant to reaching the goal state, a Sudoku puzzle is an excellent candidate for being solved as a constraint satisfaction problem by an informed agent that is able to employ one or more heuristics to guide the placement of values. One of the simplest heuristics to implement is the Minimum Remaining Values (MRV) heuristic. Most people use this heuristic when solving Sudoku problems by hand. Basically, the procedure is to search for the square that has the fewest number of possible legal values, and begin with that square. If only one legal value remains for that square, the assignment is easy. If two or more legal values are possible, some trial and error and potential backtracking will be involved, but by eliminating values that are know to violate the puzzle's constraints, the number of possible arrangements that need to be examined will be greatly reduced. The number of arrangements is further reduced by always focusing on the square with the minimum remaining values, since this has the effect of pruning away large regions of the overall search space.

In this assignment we will compare the performances of an uninformed, brute-force agent vs. an informed agent that uses the MRV heuristic, in solving Sudoku puzzles of varying difficulty. The primary measure we will use for comparing the efficiencies of the two agents will be the number of assignments attempted. This includes both correct assignments as well as those that are found to be incorrect and are discarded in the process of backtracking.

Construct a program that uses an agent to solve a Sudoku puzzle as a Constraint Satisfaction Problem, with the following guidelines:

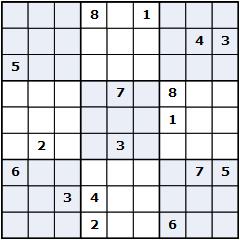
1. You may assume that only 3 x 3 Sudoku puzzles will be used. See Figure 2 for an example.
   
   
2. You may use any programming language you wish, provided I am able to compile and run your code on Windows 7. Languages I currently support include: Java, C, all .NET languages, and Python. If you wish to use a language other than this, you must run it by me ahead of time so I can make sure I can support it on my computer.
   
   
3. The program should read a Sudoku puzzle from a text file. The user should be able to browse the file system to select a puzzle file. The format of a puzzle file is as follows (comments prefaced by "//" should not appear in the file, nor should the "<blank line to indicate EOF>" text be included:
   
   9                   // puzzle width; i.e., 9 cells wide
   9                   // puzzle height; i.e., 9 cells high
   1,2,3,4,5,6,7,8,9   // domain of legal values, in the order in which they should be tried for assignments
   ---8-1---           // next 9 lines are the puzzle data
   -------43           // '-' represents an unassigned cell
   5--------
   ----7-8--
   4-----1--
   -2--3----
   6------75
   --34-----
   ---2--6--
   <blank line to indicate EOF> // blank line to indicate EOF
   
   Although I have used the digits 1-9 for the domain values, technically you may use any set of 9 distinct String values. See Figure 2 for an example of the file format minus the comments. You must follow this file format, as the test puzzles I will use to test your program will follow this format. How you represent the puzzle within your program once it has been loaded is entirely up to you.
   
   
4. You must use the standard 3 Sudoku puzzle constraints:
   1. Each row must contain a different permutation of the legal domain values.
   2. Each column must contain a different permutation of the legal domain values.
   3. Each box must contain a different permutation of the legal domain values.
      
      
5. Do not allow your agents to filter out illegal domain values prior to trying to use them — allow the constraints to perform this task.
   
   
6. While it may be tempting, do not allow your agents to use look-ahead routines or constraint propagation. Once you have completed the assignment, if you wish to go back and extend your agents by adding these capabilities, that is fine.
   
   
7. Build 2 separate agents for solving the puzzles:
   
   
   1. An uninformed, brute-force agent that attempts to solve the puzzle by starting with the first empty square and progressing from left to right, top row to bottom row. The domain of values should always be tried in the following order: 1, 2, 3, 4, 5, 6, 7, 8, 9.
      
      
   2. An informed agent that uses the MRV heuristic to determine which square to assign a value to next. The order in which cells should be assigned using this heuristic is in order of increasing number of possible values. The number of possible values for a given cell is determined by looking at the row, column, and subgrid that have that cell in common, and subtracting from 9 the number of unique values that are already present in those squares. Again, the domain of values should always be tried in the following order: 1, 2, 3, 4, 5, 6, 7, 8, 9.
      
      
   As you can see, the difference between the two agents lies in the manner in which the next cell (or variable) is selected for assignment.
   
   
8. It is up to you to decide how to model a Sudoku puzzle internally, as well as how to model the constraints.
   
   
9. To carry out the search for a solution, implement the recursive backtracking search algorithm, the pseudocode for which is shown on page 215 of the text by Norvig and Russell [3]. Use the same search algorithm for both your uninformed and informed agents.
   
   
10. To measure the relative efficiencies of the two agents, incorporate the ability to maintain counts of the total numbers of square assignments attempted. You may also keep track of the elapsed time if you wish, but counting the total number of attempted variable assignments will give an estimate of relative efficiency that is independent of hardware configuration and program implementation.
    
    
11. The output of each agent should include:
    1. The solved puzzle. (You can display this as text or using a GUI).
    2. The number of variable assignments attempted. This includes both the variable assignments that appear in the solution, as well as all the assignments that were attempted, but discarded prior to finding the solution.

Test both agents on a variety of 3 x 3 Sudoku puzzles

1. Use at least 5 different puzzles, of varying difficulties, when you test your agents. I have included a zip file containing a set of puzzles you can use, but you can also generate your own puzzles, or use puzzles you have found in Sudoku puzzle books, or on the internet.
   
   
2. Write a brief discussion of your observations, comparing the results of your two agents on each puzzle you test. Use the following questions to guide your inquiry:
   
   
   1. Did both agents find the correct solution? Given the same puzzle, did both agents find the same solution?
      
      
   2. How many variable assignments did each agent attempt before finding a solution?
      
      
   3. What happens if you change the order in which your uninformed agent attempts to assign variables? For example, if you began at the top left cell and worked your way from left to right, top to bottom, what happens if you reverse this order?
      
      
   4. How does changing the order in which the legal domain values are tried affect the performance of your agents?
      
      
   5. How is each agent's performance affected when the pre-assigned values of a puzzle are reduced in number? How does this affect the solution that is found?

	9 9 1,2,3,4,5,6,7,8,9 ---8-1--- -------43 5-------- ----7-8-- 4-----1-- -2--3---- 6------75 --34----- ---2--6--
Figure 2. An example of a 3 x 3 Sudoku puzzle. The left panel shows the puzzle graphically. The right panel indicates the proper format for representing the puzzle in the test puzzle file; '-' characters indicate unfilled squares.

1. All your source code for the project. If you used Visual Studio, please package your entire project folder into a zip file and submit that.
   
   
2. The puzzles you tested. Since you are required to write your program to read the puzzles from text files, you can simply include those text files in your submission. No points are awarded for these, but in the event I encounter problems testing your program with my own test puzzles, I will try the ones you used.
   
   
3. Your discussion of your observations.

Item	Points
Your implementation of the recursive backtracking search algorithm	15
Your uninformed, brute-force agent	15
Your informed agent using the MRV heuristic	15
Your discussion of your observations	15
Total:	60

1. Felgenhauer, B. and Jarvis, F., Mathematics of Sudoku I, http://www.afjarvis.staff.shef.ac.uk/sudoku/felgenhauer_jarvis_spec1.pdf, 2006 (last accessed 02/09/2014).
   
   
2. Russell, E. and Jarvis, F., There are 5472730538 essentially different Sudoku grids...and the Sudoku symmetry group, http://www.afjarvis.staff.shef.ac.uk/sudoku/sudgroup.html (last accessed 02/09/2014).
   
   
3. Russell, S. and Norvig, P., Artificial Intelligence A Modern Approach, Third Editiion, Pearson Education, Inc., Upper Saddle River, NJ, 2010.