
Pig is a folk jeopardy dice game described by John Scarne in 1945, and was an ancestor of the modern game Pass the Pigs® (originally called PigMania®).
The rules are simple: Two players race to reach 100 points. Each turn, a player repeatedly rolls a die until either a 1 is rolled or the player holds and scores the sum of the rolls (i.e. the turn total). At any time during a player's turn, the player is faced with two decisions:
To familiarize yourself with play, you can play an optimal Pig opponent online. The key decision facing a player is how large a turn total should be risked to possibly get an even larger total. To learn more about the game of Pig, visit The Game of Pig web page.
| Summary | Solving the Dice Game Pig - Pig, a popular folk jeopardy dice game, serves as a fun focus problem for this introduction to dynamic programming, value iteration, and basic concepts of reinforcement learning. |
| Topics | Dynamic programming, states, actions, rewards, discount factor, value iteration, reinforcement learning. |
| Audience | Introductory Artificial Intellegence students |
| Difficulty | Students selecting two exercises (1 from each set of 3 at the end of sections 2 and 3) can complete the exercises in about 1 week. For example, Pig Solitaire and Pig can be completed in less than 200 lines of Java code. |
| Strengths | Students acquire a deeper experiential knowledge of dynamic programming and value iteration through a set of fun challenge exercises that allow student choice of pursuit. Advanced exercises and recommended further lines of study are also provided. |
| Weaknesses | The presentation follows Knuth's literate programming style, and thus requires knowledge of the Java programming language. |
| Dependencies | Students must be mathematically literate, understanding summation notation, basic probability theory, and recursive definitions, as well as being comfortable with created notation. Students must also have intermediate programming skills and be familiar with Java syntax and semantics. |
| Variants | Advanced projects include analysis of the board game Risk, Yahtzee, Hog, and 10,000 (a.k.a. Farkle). Basic and advanced projects may be easily adapted to teach Monte Carlo and Temporal Difference Learning techniques. |
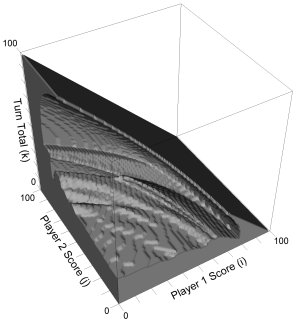
The jeopardy dice game Pig is very simple to describe, yet the optimal policy for play is far from trivial. Using the computation of the optimal solution as a central challenge problem, we introduce dynamic programming and value iteration methods, applying them to similar problems using the Java language.
The object of this project is to give the student a deep, experiential understanding of dynamic programming and value iteration through explanation, implementation examples, and implementation exercises
The student should understand
basic probability and algebraic systems of equations (although knowledge
of linear algebraic solution techniques are not required). The
student should also understand the syntax of Java. Students who
program in C++ should be able to follow most of the Java examples.
Before starting the project, the student will want to understand the
definition of a Markov decision process, perhaps by covering the
recommended background reading below.
Stuart Russell and Peter Norvig. Artificial Intelligence: a modern approach, 3rd ed. Prentice Hall, Upper Saddle River, NJ, USA, 2010.
Students are encouraged to play the game of Pig in order to have a better
understanding of the problem. An
applet with an optimal computer
player is available at the
Game of Pig
page.

The project is described in the
file pig.pdf. You will need the
free Adobe
Acrobat Reader to view this file.![]()
Example code described in the project is available here:
This code was generated from the same source file that generated pig.pdf using the literate programming tool noweb.
We recommend having students do at least one dynamic programming exercise and one value iteration exercise.
Students seeking more extended challenges will also find descriptions of related advanced projects for dynamic programming and value iteration.
Here is a sample syllabus used in CS 371 - Introduction to AI at Gettysburg College:
First class: Tuesday 9/28
Preparatory Reading: Sections 1-2 of
pig.pdf.
Dynamic programming
Homework due Thursday 9/30: One complete exercise from section 2.4
Second class: Thursday 9/30
Preparatory Reading: Remaining sections of
pig.pdf,
Russell & Norvig sections 17.1, 17.2
Value Iteration
Homework due Thursday 10/7: One complete exercise from section 3.5
(There was a two-day break 10/4-10/5. Without the break, Tuesday
10/5 rather than 10/7 would have been appropriate.)
The following additional coverage is not included in this project, but
may provide the instructor additional ideas:
Third class: Thursday 10/7:
(no preparatory reading)
Mountain Car Problem of Example 8.2 of
Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: an
introduction. MIT Press, Cambridge, Massachusetts, 1998, pp. 214-215. (Online at
http://www.cs.ualberta.ca/~sutton/book/8/node9.html
See also:
http://www-anw.cs.umass.edu/rlr/domains.html,
http://www.cs.ualberta.ca/~sutton/MountainCar/MountainCar.html
Our approach to this problem is to simply apply value iteration, discretizing the state space into a 400-by-400 grid of cells, and approximating the dynamics of each time step as a mapping from one cell to another. In other words, overlay the 2D state space (position, velocity) with a 400-by-400 grid. Simulate one time-step from each grid intersection and note which is the nearest intersection to the resulting state. This defines a mapping to discretely approximate the system dynamics. Then apply value iteration with a reward of -1 for each step that the system is not at the rightmost position.